いろいろなことを考察する

西浦氏の Scientific Reports 論文について（７）「ワクチンで感染者が９割減」は誤り

「接触8割減」の問題をまとめた論考はこちらに。
https://sarkov28.hatenablog.com/entry/2024/05/17/213470

私がネット上でしていることの まとめ は、こちらに。
https://sarkov28.hatenablog.com/entry/2022/03/29/160915


目次

（１）序論

西浦氏らのグループは、2023-10 に Scientific Reports にコロナワクチンに関する論文 [Kayano 2023a] を発表しました。
後に「コロナワクチンで死者9割以上減 京都大チームが推計」と共同が報じた論文です。（以下では [Kayano 2023a] を Sci Rep 2023 論文、と書きます。）
Evaluating the COVID-19 vaccination program in Japan, 2021 using the counterfactual reproduction number

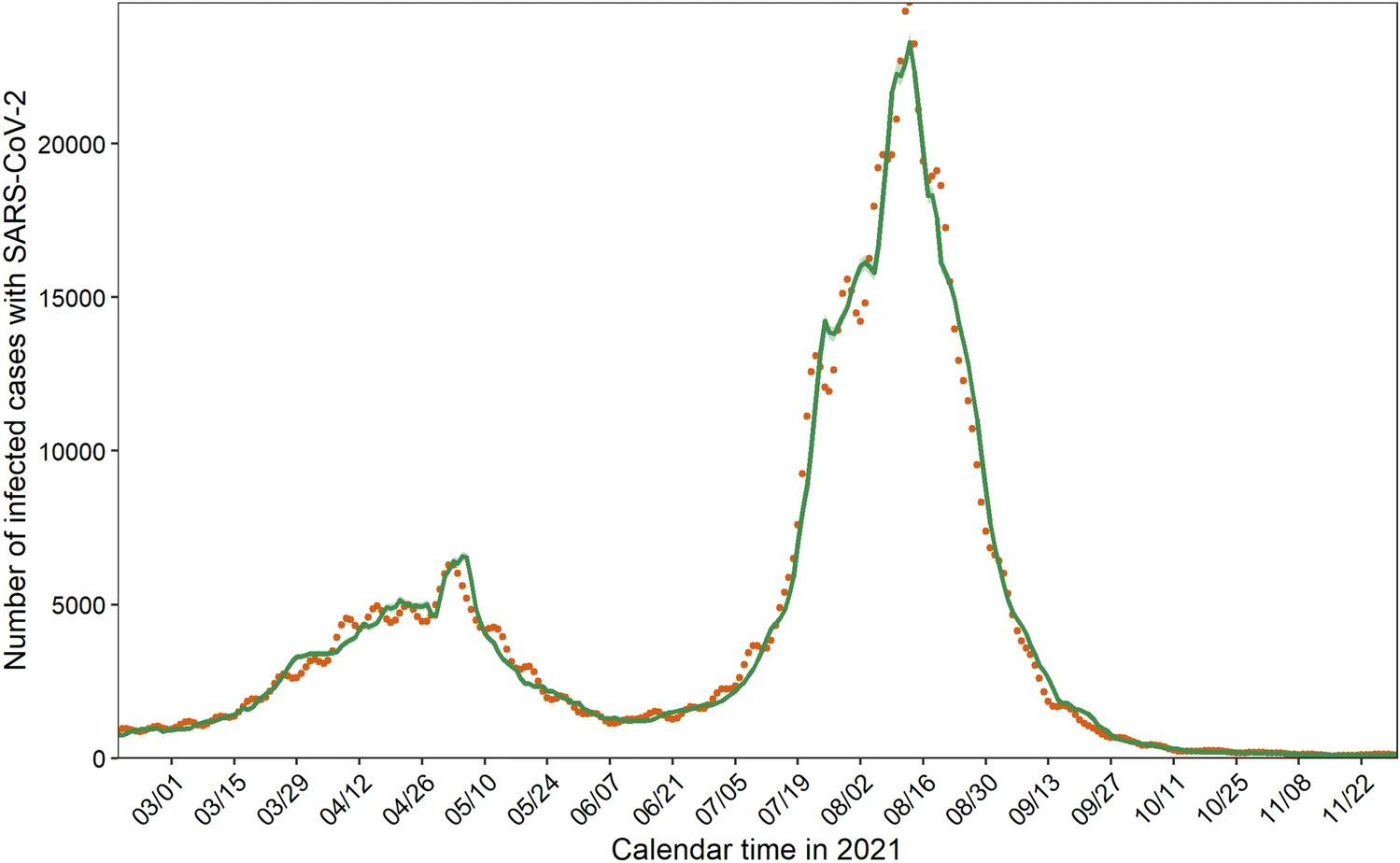
図1.1　Sci Rep 2023 論文の Figure 1
図1.1　Sci Rep 2023 論文の Figure 1（本稿の Figure 1 への言及は、限定的です。）

西浦氏は、同時期に東京のオミクロン流行時に関する論文 [Kayano 2023b] も発表しました。[Kakeya 2024] は、これらの論文におけるパラメータの信頼性の低さや、クロスバリデーションや現実データとの整合性の検証の不足を指摘しています。[Nakamura 2024a] は、[Kayano 2023b] の数理モデルに数学的不正確さなどの問題を示しています。[Nakamura 2024b] は、[Kayano 2023a] の結果の不自然さなどを述べています。[Kakeya 2024]、[Nakamura 2024a]、[Nakamura 2024b] は、Sci Rep 2023 論文 や [Kayano 2023b] についての疑問の検証のために、ソースコードの開示が必要なことを指摘しています。本稿は、Sci Rep 2023 論文の計算の前提や方法を受け入れた上で、その前提や方法に内在する限界と誤解の存在を指摘します。またこの誤解に関する誤りが社会に広がっていることを指摘します。

Sci Rep 2023 論文を引用してワクチンの効果を述べた説明には、しばしば誤りがあります。「論文のワクチンなしシナリオでの推定感染者数と、現実の感染者数とを比較し、それをワクチンの効果のように語ること」は誤りです。３つの学会（日本感染症学会、日本呼吸器学会、日本ワクチン学会）が連名で発表した見解が Sci Rep 2023 論文に言及した部分は、この誤りに陥っています。

これは Sci Rep 2023 論文に関する典型的な誤りでもあるので、本稿は、これが誤りであることを説明します。同様の誤りが、西浦氏の SNS 投稿や産経記事、Sci Rep 2023 論文にあることも示します。 この論文は、非常に特殊なシナリオでの感染状況を計算しています。このシナリオは不自然で非現実的なものです。計算結果は現実に起きる可能性がないものであり、また過大であることが分かっています。

（２）節では、例えを用いて論文のシナリオが不自然で非現実的であること、計算結果の感染者数が過大であることを示します。 （３）節では、「論文の感染者数と現実の感染者数を比較する誤り」を示し、この誤りが生まれる背景を検討します。 （４）節では、ワクチンなしシナリオの不自然さが解消不可能であることを示します。 （５）節では、ワクチンなしシナリオの不自然さを、この論文も実質的に説明していることを示します。 （６）節では、（３）節の誤りの実例として、Sci Rep 2023 論文、西浦氏の x.com への投稿、産経記事、３つの学会の見解、における誤りを説明します。 （７）節では、論文について述べた西浦氏のスレッドを検討します。 （８）節では、論文の意義について再検討します。 （９）節では、論文への誤解の原因と、西浦氏の責任について検討します。 （１０）節では、政府や企業の対策に関するこの論文の問題点を述べます。 （１１）節では、[Kayano 2023b] にも Sci Rep 2023 論文と同様の問題があることを説明します。 （１２）節では、結論を述べます。

この論文については、複数の記事で書いています。

（記事（７）と記事（１）とは重なる事項を検討しているため、一部に重複があります。）

（２）雨と傘の例え

（２）節では、「雨と傘の例え」を用いて、この論文のシナリオが不自然で非現実的であることを説明します。

(2-1) 雨と傘の例えの対応表と Sci Rep 2023 論文のシナリオ

Sci Rep 2023 論文の「ワクチンなしシナリオ」は、感染が現実より大幅に拡大しても、人々が行動を変えないという非現実的な想定に基づいています。本節では、このシナリオの不自然さを「雨と傘の例え」を用いて説明します。

この例えでは、感染症の状況を「雨の強さ」、感染症への感染を「雨にかなり濡れること」、ワクチンによる感染予防効果を「傘」、個人の感染予防行動を「雨を避ける行動」に例えます [注2-1a]。

表2-1 「雨と傘の例え」の対応表

コロナとワクチンの状況 雨と傘の例え
コロナの状況 雨の強さ
　現実（ワクチンあり）
　でのコロナの状況		 　小雨
　ワクチンなし
　でのコロナの状況		 　大雨
コロナへの感染 雨にかなり濡れること
ワクチンによる
感染予防効果		 傘
ワクチン以外の
個人の感染予防行動		 雨を避ける行動
（外出を控える、
　移動手段を工夫するなど）


この例えは、雨にかなり濡れた人が増加した理由が1つ（「傘がなくなったこと」）ではなく、2つ（「傘がなくなったこと」と「不自然な行動をしたこと」）であることを確認するために示しています。これが確認できると、「論文のワクチンなしシナリオの想定の非現実性」や「計算される感染者数が過大であること」が確認できます。

ワクチンあり（傘あり）の現実的シナリオでのある日は、「雨と傘の例え」では以下になります。

小雨で（コロナの状況が現実と同じで）、６割の人が傘を差しています（ワクチンによる免疫を持っています）。傘を持っていない人（ワクチンによる免疫がない人）も４割いて、その人たちは雨を避けます（感染を避けます）が、一部の人は、雨にかなり濡れました（感染しました）。

ここでの人々の行動に不自然なところはありません。（ワクチンによる免疫を持つ人が６割の状況を想定しています。）

ワクチンなし（傘なし）の反事実仮想シナリオでの同じ日は、Sci Rep 2023 論文の考え方では以下になります。

大雨で（コロナが大幅に（現実の１０倍以上に）拡大した状況で）、傘を差している人（ワクチンによる免疫がある人）は一人もいません。しかし６割の人は、傘を持っている時と同じ行動をする（行動を変えない）ので、雨にかなり濡れる人（感染する人）がいました。また、４割の人は雨を避けますが（感染を避けますが）、その避け方は、大雨が降っているのに小雨が降っている時と同じなので（感染が大幅に拡大した状況なのに現実と同じなので）、雨にかなり濡れる人（感染する人）がいました。

ここでの人々の行動は不自然です。状況が（雨が、感染状況が）変わっているのに行動を変えないからです。

ワクチンなし（傘なし）シナリオでの人々の行動は不自然です。Sci Rep 2023 論文はこの不自然な状況で感染者数（雨にかなり濡れた人数）を数えているので、この論文が計算する感染者数は不自然な値になります。

この例えには限界があります。この例えで考えても、雨にかなり濡れた人の増加が、2つの理由（「傘がなくなったこと」と「不自然な行動をしたこと」）のどちらにどの程度起因するのかを判断することはできません。したがってどちらが主因なのかを検討することもできません。この例えで行えるのは、雨にかなり濡れた人が増加した理由が1つ（「傘がなくなったこと」）ではなく、2つである、ということの確認です。

またこの例えは、いわゆる感染症の従属性は表現できません。例えが「ある日の」などと時間を区切っているのはこの点に対応するためです。ある日のワクチンなしシナリオが不自然で非現実的であることが示せれば、この例えの目的は済んでいます。


[注2-1a] Sci Rep 2023 論文は、ワクチンを接種すると（時間が経過すると減衰するが）感染予防効果を得られるという考え方を採っています [注2-1b]。またこの論文は、人々の行動の変化が実効再生産数に影響を与えると考えています [注2-1c]。本稿はこれらの考え方で考えます。本稿が、「Sci Rep 2023 論文と同様に考えた場合の問題点を検討する」という方針だからです。
[注2-1b] Sci Rep 2023 論文は、式(1) で計算したワクチンの効果 l_{a,t} を式(3) で使っています。式(1) の計算結果は、補足情報（41598_2023_44942_MOESM1_ESM.docx）の Supplementary Figure S2 に示されています。
[注2-1c] Sci Rep 2023 論文は、人々の活動度 h_t を式(4) で計算し、式(3) で使っています。関連するグラフとして、補足情報（41598_2023_44942_MOESM1_ESM.docx）の Supplementary Figure S4 があります。

(2-2) ワクチンなしシナリオの感染者数は過大

Sci Rep 2023 論文の「ワクチンなしシナリオ」では、感染が現実より大幅に拡大しても、人々の行動が変わらないと想定しています。この非現実的な想定によって、推定される感染者数が過大になっています。本節では、このシナリオの感染者数が過大である理由を「雨と傘の例え」を用いて説明します。

(2-1)節 で示したように、ワクチンなし（傘なし）シナリオでの人々の行動は以下でした。

「雨と傘の例え」で考えると：

  • ６割の人は大雨で傘を持っていないのに、小雨で傘を持っていた時と同じ行動をする。
  • ４割の人の雨の避け方は（大雨が降っているのに）小雨が降っている時と同じである。

コロナとワクチンで考えると：

  • ６割の人はコロナが大幅に拡大してワクチンによる免疫がないのに、現実の感染状況でワクチンによる免疫がある時と同じ行動をする。
  • ４割の人の感染の避け方は（コロナが大幅に拡大した状況なのに）現実の感染状況の時と同じである。

ここには不自然な行動があります。この状況で増えた感染者数（雨にかなり濡れた人数）には、不自然な行動を原因とする人数が含まれています。したがって、ワクチンなしシナリオでの感染者数は過大になっています。 このことは、論文の限界事項（limitations）に記載されるべきですが、論文にその記述はないので不適切です。

Sci Rep 2023 論文のワクチンなしシナリオでの感染者数が過大だとしても、それがどの程度過大なのかは不明です。どの程度過大なのかを計算するためには、（４）節 で検討する「人々が感染拡大に対してどう行動を変えるかの予測」と「その行動変化による実効再生産数の変化の数値的な予測」が必要です。これらを予測する方法は実質的にないので、この論文の感染者数がどの程度過大なのかを計算することはできません。

(2-3) 感染者数と死者数での同じ問題の発生

Sci Rep 2023 論文では、感染者数に IFR（感染者致死率）を乗じて死者数を計算しています。この計算は、年齢層ごとに行われ、各年齢層の死者数は、その年齢層の感染者数に比例します。ただし、全年齢層の死者数は、全年齢層の感染者数に比例はしません。年齢層ごとにIFRが異なるためです。

年齢層ごとの死者数はその年齢層の感染者数に比例するので、各年齢層の感染者数で起きた（(2-2)節 で論じた過大さのような）な問題は、死者数でも同様に生じます。この関係は各年齢層で成立するので、全年齢層での感染者数と死者数でも同様の問題が生じます。

本稿は感染者数や死者数の具体的な数値の正確性を論じるものではなく、計算における構造的な問題を指摘しようとしています。このため、年齢層ごとの詳細な議論を省略しても、指摘している問題の妥当性に影響はありません。

また本稿は、主に感染者数の問題を議論しますが、Sci Rep 2023 論文の計算方法では、感染者数と死者数で同じ問題が成立します。感染者数が過大ならば死者数も同様に過大です。感染者数がどの程度過大なのかが不明であれば、死者数がどの程度過大なのかも不明です。

(2-4) 本稿への疑問に(1) 論文の「反事実仮想 counterfactual シナリオ」は非現実的

(2-1)節 に対し、以下のような疑問があるかも知れません。

(2-1)節 は、Sci Rep 2023 論文のワクチンなしシナリオが非現実的などと説明している。しかしもともと論文は、ワクチンなしシナリオを「反事実仮想 counterfactual シナリオ」と記述している。(2-1)節 の指摘は論文の意図を説明しているだけでは。当たり前のことを述べているだけでは。

確かに論文は、ワクチンなしシナリオなどを反事実仮想シナリオと記述しています。しかし、(2-1)節 が示しているのは、これが単なる「事実と異なるシナリオ」ではなく、「現実性が全くないシナリオ」だということです。

図2.1 は、「シナリオ全体の集合」を3つの集合

  • 「現実的なシナリオの集合」
  • 「現実性が乏しいシナリオの集合」
  • 「現実性が全くないシナリオの集合」

に分け、これらの集合に属する要素である

  • 「（ワクチン接種があった）現実」
  • 「現実社会にワクチンがなかったら、どうなっていたのかのシナリオ」
  • 「論文のワクチンなしシナリオ」

を、(2-1)節～(2-3)節 の考え方で配置したものです。


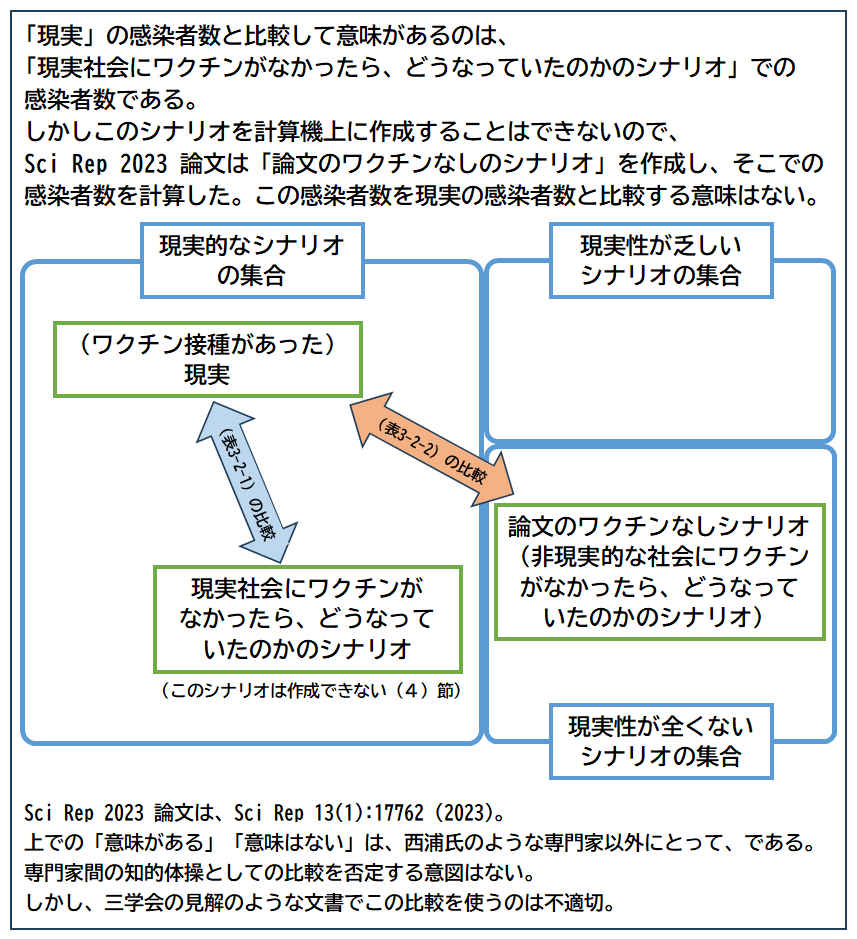
図2.1　3つのシナリオの、3つの集合における位置

論文の「反事実仮想シナリオ」である「ワクチンなしシナリオ」は、(2-1)節 に示したように非現実的なシナリオです。このシナリオの非現実性は、「たまたま現実とは違うが、偶然が重なれば現実がこうでもおかしくない」（＝現実的なシナリオ）や「現実性は乏しいが、もしかしたらこういうことがあるかも知れない」（＝現実性が乏しいシナリオ）における非現実性とは異なります。

「ワクチンなしシナリオ」の非現実性は、現実性が全くないという非現実性です。この非現実性は、論文では明確になっていませんでしたが、(2-1)節 は、このことを明確に示しました。したがって、本節冒頭に示した「(2-1)節 が論文の意図を説明しているだけでは」との疑問は、妥当ではありません。

(2-5) 本稿への疑問に(2) 論文は「全ての行動が変わらない」を実質的に前提している

(2-1)節 に対し、以下のような別の疑問があるかも知れません。

(2-1)節 は、Sci Rep 2023 論文の「ワクチンなしシナリオ」が「状況が変化しても、全ての行動が変わらない」を前提しているかのように述べている。しかしそのような前提は論文に記載がない。(2-1)節 は、勝手な前提を作り上げてそれを批判しているのでは。

説明が長くなるので上では書きませんでしたが、その疑問は次のように考えれば解決します。

「状況が変化しても、行動が変わらない」は、「状況が変化しても、実効再生産数に影響を与える行動変容はない」を意味している。

状況が変化した時の人々の行動を、「実効再生産数に影響を与える行動」と「実効再生産数に影響を与えない行動」に分けます。後者の影響を与えない行動は、実効再生産数に影響を与えないのですから、論文や本稿が考慮する対象から除外しても論旨に影響を与えません。

一方前者について論文は、「状況が変化しても、実効再生産数に影響を与える行動変容はない」を前提しています。これは論文式(3)から分かります。もしも「状況が変化したら、実効再生産数に影響を与える行動変容がある」と論文が前提しているなら、該当の項が論文式(3)の右辺に必要です。その項がないと等式が成立しなくなるからです。しかしそのような項はそこに存在しません。

したがって論文は式(3)で、「状況が変化しても、実効再生産数に影響を与える行動変容はない」と述べています。

したがって本節冒頭に示した「(2-1)節 は勝手な前提を作り上げてそれを批判しているのでは」との疑問は、妥当ではありません。

（３）論文の感染者数と現実の感染者数を比較する誤り

(3-1) ワクチンなしシナリオについての誤った印象

「ワクチンを接種していないシナリオ」と聞くと、つい「ワクチンを接種しない想定だが、そこでの人々の行動は、常識的で自然なものを想定したシナリオ」だと考えてしまうかも知れません。しかし、それは誤解です。

Sci Rep 2023 論文のシナリオはそうした現実的なものではありません。 この論文のワクチンなしシナリオは、(2-1)節 で述べたように「ワクチンを接種しない想定だが、感染が現実より大幅に拡大しているにもかかわらず、人々が行動を変えないというシナリオ」です。

この論文が想定しているワクチンなしシナリオが、このように不自然で非現実的なものになる直接の原因は、論文の「状況が大きく変化しても人々は行動を変えない」との想定が不自然で非現実的だからです。

(3-2) 感染者数比較の誤り：本来あるべき比較

Sci Rep 2023 論文のように「ワクチン接種で感染予防効果が得られる」と考えるなら、

疑問〈3-2a〉
「この社会にもしワクチンがなかったら、感染者数や死者数はどうなっていたのか」

という疑問が出てくるのは自然です。しかしこの論文の推定感染者数は、この疑問への回答になりません。

表3-2-1 は、疑問〈3-2a〉に回答するための、本来の比較です。

表3-2-1 「この社会にもしワクチンがなかったら、感染者数や死者数はどうなっていたのか」のための比較

ワクチンあり ワクチンなし
ワクチン あり なし
状況が変化した時の
人々の行動指針		 状況に応じて
柔軟に行動を変える		 状況に応じて
柔軟に行動を変える

ワクチンなしでの感染者数と現実の感染者数を比較するなら、この比較を行う必要があります。

状況に応じて行動が変わるのが自然な人間の姿です。状況が変わっても行動が変わらないのは不自然です。 表3-2-1 の左右で違うのはワクチンの有無だけなので、この左右での感染者数を比較すれば、疑問〈3-2a〉への答えになると期待できます。

一方、Sci Rep 2023 論文の推定感染者数を使った比較は、以下になります。

表3-2-2 Sci Rep 2023 論文を使った比較

ワクチンあり ワクチンなし
ワクチン あり なし
状況が変化した時の
人々の行動指針		 状況に応じて
柔軟に行動を変える		 状況が変化しても
行動を変えない

Sci Rep 2023 論文が計算した感染者数と現実の感染者数の比較は、この比較になります。

「Sci Rep 2023 論文を使った比較」のワクチンなしシナリオは、状況が変化しても（感染状況が現実の１０倍以上に拡大しても）人々の行動は変化しないシナリオです。これは人間の行動にあるはずの性質を欠いた奇妙なシナリオです。そして「Sci Rep 2023 論文を使った比較」では、ワクチンの有無だけでなく、状況が変化した時の人々の行動の方針も異なります。この条件で感染者数を比較しても、疑問〈3-2a〉への答えにはなりません。

以上の検討により、

疑問〈3-2a〉
「この社会にもしワクチンがなかったら、感染者数や死者数はどうなっていたのか」

という自然な疑問に回答するための比較として、「Sci Rep 2023 論文を使った比較」が間違いであることが分かります。論文の推定感染者数と現実の感染者数の比較（表3-2-2）では、疑問〈3-2a〉への答えにはなりません。比較として適切なのは、本来の比較（表3-2-1）です。

(3-3) Sci Rep 2023 論文が答えている疑問とは

(3-2)節 での検討は、自然な疑問である

疑問〈3-2a〉
「この社会にもしワクチンがなかったら、感染者数や死者数はどうなっていたのか」

との疑問に Sci Rep 2023 論文が答えていないことを示しています。「Sci Rep 2023 論文を使った比較（表3-2-2）」ではこの疑問に回答できないからです。

一方で、この論文が答えている疑問（＝「Sci Rep 2023 論文を使った比較（表3-2-2）」が答えられる疑問）は以下です。

疑問〈3-3a〉
「感染規模が現実の１０倍以上に拡大しても現実と同じ行動をする、との不自然な社会に、もしワクチンがなかったら、感染者数や死者数はどうなっていたのか」

これは、疑問〈3-2a〉とは全く違う疑問です。Sci Rep 2023 論文は、ほとんどの人が問わない疑問（疑問〈3-3a〉）に答えています。そして、自然な疑問（疑問〈3-2a〉）に答えていると誤解されています。

Sci Rep 2023 論文が計算しているのは、現実の社会のワクチンの効果ではなく、不自然な社会でのワクチンの効果です。

(3-4) 感染者数比較の誤り：例えによる説明

(3-2)節・(3-3)節 での検討と重なる内容を、例えを用いて説明します。（ここまでで納得した方は読む必要がないかもしれません。）

「雨と傘の例え」における、傘ありシナリオで雨にかなり濡れた人数と、傘なしシナリオで雨にかなり濡れた人数とを比較して、「これが傘の効果です」と述べるのは誤りです。

傘なしシナリオで雨にかなり濡れた人が増加したのは、傘がなかったことが原因の一つです。しかし、それだけではありません。６割の人が、大雨で傘を持っていないのに、小雨で傘を持っていたときと同じ行動をしたことも原因です [注3-4a]。
雨にかなり濡れた人の増加が、傘がなかったことが原因であるかのように（あるいはそれが主因であるかのように）述べるのは誤りです。雨にかなり濡れた人数を両者で（傘ありシナリオと、傘なしシナリオとで）比較して、それを傘の効果だと示すことはできません。傘の他にも理由があるからです。

同様に、現実の推定感染者数と、ワクチンなしシナリオでの推定感染者数とを比較して、「これがワクチンの効果です」と述べるのは誤りです。
ワクチンなしシナリオで感染者数が増加したのは、ワクチンによる免疫がなかったことが原因の一つです。しかし、それだけではありません。６割の人が、感染が大幅に拡大した中でワクチンによる免疫がないのに、現実の感染状況でワクチンによる免疫があったときと同じ行動をしたことも原因です [注3-4b]。
感染者の増加が、ワクチンによる免疫がなかったことが原因であるかのように（あるいはそれが主因であるかのように）述べるのは誤りです。推定感染者数を両者で（現実とワクチンなしシナリオとで）比較して、それをワクチンの効果だと示すことはできません。ワクチンの他にも理由があるからです。


[注3-4a] 雨にかなり濡れた人が増加した原因には、４割の人の不自然な行動（大雨なのに小雨の時と同じ行動をした）もあります。
[注3-4b] 感染者数が増加した原因には、４割の人の不自然な行動（感染が大幅に拡大しているのに現実と同じ行動をした）もあります。

(3-5) 論文の感染者数と現実の感染者数を比較する誤り

(3-2)節～(3-4)節 での検討を踏まえて、Sci Rep 2023 論文に関してしばしば見られる誤りを確認します。

〈3-5a〉論文の感染者数と現実の感染者数を比較する誤り
Sci Rep 2023 論文のワクチンなしでの推定感染者数と、現実の推定感染者数とを比較して、「これがワクチンの効果です」と述べるのは誤りです。

この論文を根拠としたワクチンの効果が各所で述べられているのですが、それはしばしば、この誤りに陥っています。

この誤りの実例は、（６）節 で示します。

なお、〈3-5a〉で、「現実の感染者数」ではなく「現実の推定感染者数」と書いたのは、以下の理由からです。Sci Rep 2023 論文は、全体の感染者のうち一部だけが報告されていると考えていて、その比率を感染者報告率 reporting coverage としています。論文でのこのパラメータの主な値は、0.25 です。この場合、報告感染者数を 0.25 で割り算して全体の感染者数を推定します。論文のワクチンなしでの推定感染者数と比較されているのは、報告感染者数そのものではなく、この 0.25 で割り算した値です。これは推定値なので、「現実の感染者数」ではなく「現実の推定感染者数」と書いています。

（４）ワクチンなしシナリオの不自然さは解消できない

(4-1) ワクチンなしシナリオの不自然さは解消できない

ワクチンなしシナリオに「ワクチンなしでも行動を変えない」という不自然なところがあるなら、不自然さを取り除いたシナリオにすればいいと考える人がいるかもしれません。しかし残念ながら、この不自然さを取り除くことはできません。

この不自然さを取り除くためには、「ワクチンなしシナリオで感染拡大した時には人々が行動を変える」とのシナリオで感染者数を計算することになります。このシナリオで感染者数を計算するには、人々が感染拡大に対してどう行動を変えるかを予測した上で、その行動変化による実効再生産数の変化を数値的に予測する必要があります。

これらの予測は現在のところ実質的に不可能です。（これらを予測しようとの試みはあるかも知れませんが、Sci Rep 2023 論文が不自然さを取り除いたシナリオを作成できるような成果は得られていません。）論文が「ワクチンなしでも行動を変えない」という不自然な想定を採用したのは、これが理由だと思われます。

同じことですが、ワクチンなしシナリオには、ワクチンを接種しなかった場合に現実の社会がどうなるかをモデル化しようとの意図は最初からなかったはずです。これが不可能であることは、西浦氏らには分かっていたはずだからです。現在の理論疫学ではそのようなモデル化はできないので（他のシナリオを作る方法がないので）、西浦氏は不自然で非現実的な想定のシナリオを作成し、そこでの感染者数を計算したと思われます。

(4-2) 実効再生産数を変更した計算

(4-1)節 でワクチンなしシナリオの不自然さを解消できなかった一つの要因は、「行動の変化がどのように実効再生産数の変化」に結びつくかが不明だから」でした。この不明な部分を回避した、「実効再生産数が変化したら」というシナリオならば作成できます。そしてこのシナリオでの感染者数は計算できます。

つまり、「〇月〇日～〇月〇日で、実効再生産数が 0.5 下がったら」あるいは「実効再生産数が 0.5 倍になったら」などのシナリオです。

しかしこのように作成したシナリオが、実際の感染症対策に有効であるとは考えにくいです。なぜなら、これらのシナリオが前提とする「実効再生産数を 0.5 下げる（0.5 倍にする）」という感染症対策が具体的に何なのかは、不明だからです。（特定の感染症対策が実効再生産数にどのような影響を与えるのかを定量することもできません。）このように「実効再生産数を 0.5 下がったら（0.5 倍になったら）」というシナリオには別の問題が発生するので、本質的な解決になりません。

（５）ワクチンなしシナリオの不自然さを示す、Sci Rep 2023 論文の記述

「雨と傘の例え」で、ワクチンなしシナリオが不自然であることを示しました。しかし納得していない方がいるかも知れません。「そんな結論になるのは「雨と傘の例え」におかしなところがあるからではないか」と。

そうした疑問に答えるため、西浦氏が実質的に同じ内容を Sci Rep 2023 論文で述べていることを説明します。 なお、ここで示すことと同じ内容を、西浦氏は x.com への投稿でも述べていますが、この投稿については後の (7-3)節 で述べます。

(5-1) 説明の準備

説明のために確認しておくことがあります。
Sci Rep 2023 論文のワクチンなしシナリオが不自然なシナリオになるのは、このシナリオが「他の条件は全て同一で、ワクチン接種率だけをゼロにしたシナリオである」からです。この「他の条件が全て同一で」という部分が、「コロナ感染が大幅に（実際の１０倍以上に）拡大した状況でも、同じ行動をする」という不自然さに現れます。

したがって、

〈5-1a〉ワクチンなしシナリオは、他の条件は全て同一で、ワクチン接種率だけをゼロにしたシナリオである。

を示せば、

〈5-1b〉Sci Rep 2023 論文のワクチンなしシナリオは不自然な想定のシナリオである。

を示したことになります。

(5-2) ワクチンなしシナリオの不自然さを示す、Sci Rep 2023 論文の記述

（この (5-2)節 は本文中に数式が入りますが、数式部分を飛ばして読んでも大きな影響はないようにしています。）
Sci Rep 2023 論文の式(1) と式(3) は以下です。

\displaystyle l_{a,t} = \frac{1}{n_a} \sum_{s=1}^{t-1}\ v_{a,t-s}\ h_s\ \ ...\ \ 式(1)

\displaystyle R_{ab,t} = \left( 1 - l_{a,t} - \frac{\sum_{k=1}^{t-1} i_{a,k}}{n_a} \right) K_{ab}\ p\ h_t\ d_t\ c_t\ \ ...\ \ 式(3)

式(1) の v_{a,t} は年齢層 a、時刻 t のワクチン接種者数です。（" v_{a,t} denotes the number of vaccinated individuals in age group a at calendar time t,"）ワクチンなしシナリオではワクチン接種者がいないと考えるのですから、 v_{a,t} は、全ての a、t において v_{a,t} = 0 になります。すると式(1) から、この場合の l_{a,t} は、全ての a、t において l_{a,t} = 0 になります。

したがって、式(3) のうち l_{a,t} は常に 0 になります。他の変数の値は変化しません。 これは、〈5-1a〉の 「他の条件が全て同一で、ワクチン接種率だけをゼロにしたシナリオ」 を、数式で表現したものです。「他の条件が全て同一」が「他の変数の値は変化しない」に対応し、「ワクチン接種率だけをゼロ」が「 l_{a,t} は常に 0」に対応しています。

つまり Sci Rep 2023 論文は、〈5-1a〉を述べています。

〈5-1a〉ワクチンなしシナリオは、他の条件は全て同一で、ワクチン接種率だけをゼロにしたシナリオである。

論文は〈5-1a〉を述べているのですから、(5-1)節 で準備したように、〈5-1b〉を述べていることになります。

〈5-1b〉Sci Rep 2023 論文のワクチンなしシナリオは不自然な想定のシナリオである。

（６）「論文の感染者数と現実の感染者数を比較する誤り」の例

Sci Rep 2023 論文は誤解されやすい論文です。実際、日本社会に広がったのは (3-5)節 に示した誤り〈3-5a〉でした。

〈3-5a〉論文の感染者数と現実の感染者数を比較する誤り
Sci Rep 2023 論文のワクチンなしでの推定感染者数と、現実の推定感染者数とを比較して、「これがワクチンの効果です」と述べるのは誤りです。

（６）節では、この誤りの具体例を取り上げます。

  • (6-1)節：Sci Rep 2023 論文におけるこの誤りについて検討します。
  • (6-2)節：西浦氏の x.com への投稿におけるこの誤りについて検討します。
  • (6-3)節：産経新聞の記事に、この誤りがあることを示します。
  • (6-4)節：西浦氏によるその記事の紹介が不適切であることを説明します。
  • (6-5)節：日本感染症学会、日本呼吸器学会、日本ワクチン学会の見解に含まれるこの誤りを指摘します。

(6-1) Sci Rep 2023 論文における誤り

Sci Rep 2023 論文の中に、「論文の感染者数と現実の感染者数を比較する誤り」 に該当する記述があります。二つを挙げます。

In the absence of vaccination, the cumulative numbers of infections and deaths during the study period were estimated to be 63.3 million (95% confidence interval [CI] 63.2–63.6) and 364,000 (95% CI 363–366), respectively; the actual numbers of infections and deaths were 4.7 million and 10,000, respectively.
（ワクチン接種を実施しなかった場合、調査期間中の累積感染者数は6,330万人（95％信頼区間［CI］63.2-63.6）、死亡者数は36万4,000人（95％CI 363-366）と推定されたが、実際の感染者数は470万人、死亡者数は1万人であった。）


A critical take-home message from the present study is that the indirect effect of vaccination was enormous in Japan. The numbers of prevented infections and deaths were 13.5 and 36.4 times the empirically observed counts, respectively.
（本研究から得られる重要な結論は、日本におけるワクチンの間接効果が非常に大きかったという点である。予防された感染者数と死亡者数は、それぞれ実測値の13.5倍と36.4倍に達した。）

どちらも論文の推定感染者数を実際の感染者数と比べているので、「論文の感染者数と現実の感染者数を比較する誤り」 に該当しています。

「論文は、推定感染者数が現実的な数値だという意味でその比較をしているのではない。ワクチンなしシナリオについての記述を読めば、シナリオが不自然で非現実的であることは分かるから、誤解する方がおかしい」との主張があるかも知れませんが、その主張は成立しません。

なぜならその誤解を避けるための論文の説明は明らかに不十分だからです。(6-5)節 に示すように３つの学会の見解も 「論文の感染者数と現実の感染者数を比較する誤り」 に陥っています。専門家の集団である学会が誤解するほど、論文の説明は誤解しやすく分かりにくいのです。

Sci Rep 2023 論文のワクチンなしシナリオでの推定感染者数や死者数は、シナリオが不自然で非現実的であるとの分かりやすい説明が不十分な状態で示されています。この論文のこれらの記述は、少なくとも誤解の恐れが極めて大きいものであり、不適切です。

(6-2) 西浦氏の x.com への投稿における誤り

西浦氏は、2023-10-18 に Sci Rep 2023 論文についての投稿を x.com にしています。 https://x.com/nishiurah/status/1714629177385553981

京大と感染研の共同。反事実仮想を実効再生産数の成分で作成し、2021年予防接種2回が仮に無かった時の流行を作り因果推論を実施。2021年2月～11月末で6330万(6320-6360万）が感染し36.4万人が死亡する計算になり、実際には470万人感染・1万人死亡。差分は予防接種で逃れた。https://t.co/YqR0CshH0G

この投稿は、論文の推定感染者数を、現実の感染者数と比較しているので、「論文の感染者数と現実の感染者数を比較する誤り」 に該当しています。

西浦氏は「反事実仮想を作成し」と述べていますが、これは論文の想定が不自然で非現実的であることを充分に説明していません。一方で西浦氏は「逃れた」と記述していて、これはあたかも「実際に感染を回避した人数を論文が示している」かのようです。

このような投稿は、誤解を招くものであり、不適切です。

なおこの投稿の記述には、論文の記述とやや不整合なところがあります [注6-2a]。


[注6-2a] 西浦氏の投稿の記述は、論文の「13.5倍」「36.4倍」とやや不整合なので、どちらかが誤っています。周辺の事情から考えると、「13.5倍」について誤っているのは論文の記述だと思われます。

(6-3) Sci Rep 2023 論文を紹介した産経の記事の誤り

産経は、2023-11-16 の記事「新型コロナワクチンで死者９割以上減　京都大推計」（同アーカイブ）で Sci Rep 2023 論文について報じました [注6-3a]。

この記事は、論文の推計結果だとして、ワクチンの接種によって研究期間中の感染者数と死者数を「いずれも９０％以上減らせた」と説明しています。この表現は論文の推定感染者数を、現実の感染者数と比較しているので、(3-5)節 に示した「論文の感染者数と現実の感染者数を比較する誤り」 に陥っています。よってこの記事は不適切です。

この記事には論文がどのような想定で計算されたかについての詳しい説明はありません。その結果、一般読者は示された感染者数や死者数を現実的な値と誤解し、ワクチンの効果を過大評価する恐れがあります。

このため、ワクチンの効果を過度に評価してしまう可能性があります。ワクチンは国民の健康に関する事項ですから、一般の読者に向けた記事は正確性において慎重であるべきです。この記事は慎重とは言えませんから、不適切です。


[注6-3a] 産経記事は共同通信からの配信によっていると思われ、ネット上には 共同記事 もありました。共同記事は現在はリンク切れです。アーカイブ をご参照下さい。共同記事と産経記事の差はほとんどありません。

(6-4) 産経記事を紹介した西浦氏の投稿の問題

(6-3)節 で不適切だと説明した産経記事を、西浦氏は x.com への投稿で「ぜひ多くの方に読んでいただきたい」と紹介しました。2023-11-16 の投稿 https://x.com/nishiurah/status/1725101388987019748 です。

共同通信からの配信です。ぜひ多くの方に読んでいただきたいニュースです「新型コロナワクチンで死者９割以上減　京都大推計」 https://sankei.com/article/20231116-3ICUWGMN3FMVZNSKJJGKPB4ARE/

西浦氏はこの投稿で、「新型コロナワクチンで死者９割以上減」との記事タイトルを拡散しました。しかし (6-3)節 に述べたように、この記事には Sci Rep 2023 論文の不自然な想定の詳しい説明がなく、西浦氏の投稿にもその説明はありません。したがって西浦氏の投稿は不適切であり、一般読者が記事と同じ「論文の感染者数と現実の感染者数を比較する誤り」 に陥る可能性や、ワクチンの効果を過大評価する可能性を招いています。またそれを「多くの方」に拡散しています。

(6-5) 日本感染症学会、日本呼吸器学会、日本ワクチン学会の見解の誤り

日本感染症学会、日本呼吸器学会、日本ワクチン学会（以下、三学会と略記します）は、2024-10-17 に「2024年度の新型コロナワクチン定期接種に関する見解」 を発表しました。

このうち Sci Rep 2023 論文に関する付近を引用します。

わが国でも、新型コロナワクチンが導入されていなかったら、2021年2月から11月の期間の感染者数は報告数の13.5倍、死亡者数は36.4倍であったと推定されています { }^{2)}。また、オミクロン株流行期の2022年1月から5月の東京都でも、直接的・間接的に感染者数を65%減少させたと報告されています { }^{3)}。[注6-5a] [注6-5b]

引用部では、論文を参考文献に挙げながら「ワクチンがなければ感染者は報告数の13.5倍、死亡者数は36.4倍であった」との推定が示されています。これは、論文が推計した感染者数と現実の感染者数とを比較しているので、(3-5)節 に示した「論文の感染者数と現実の感染者数を比較する誤り」 に陥っています。

したがって見解のこの箇所は不適切です。見解の表現では、読者や政策決定者がワクチンの効果を過大評価してしまう恐れがあります。 見解がこの論文の計算結果を用いるなら、誤解を避けるために、この論文が不自然で非現実的な想定で計算していることを明確にし、専門家の学会としての責任を果たす必要があります。

また、この見解には 概要 も示されています。見解の概要も、Sci Rep 2023 論文を示しながら「わが国でも2021年2～11月の死亡者数を大きく減少させたとされています」と述べていて、この記述は「論文の感染者数と現実の感染者数を比較する誤り」に陥っています。概要のこの箇所は不適切です。

この見解には西浦氏の別の論文 [Kayano 2023b] に関する問題もあります。この件については（１１）節 で検討します。


[注6-5a] 引用中、"2)" で参照されているのは Sci Rep 2023 論文 [Kayano 2023a] です。"3)" で参照されているのは [Kayano 2023b] です。
[注6-5b] 見解の記述「13.5倍」「36.4倍」は、[注6-2a] に示した不整合に関するものです。三学会の見解は、(6-2)節 の西浦氏の投稿と整合しています。論文、西浦氏の投稿、三学会の見解のうち、誤っているのは論文だと思われます。

（７）Sci Rep 2023 論文について述べた西浦氏の投稿の検討

西浦氏は、2023-11-01 の x.com に 論文についてのスレッドを投稿しました。このスレッドの3つの投稿を順に検討します。

(7-1) 一つ目の投稿

一つ目の投稿はこちら（[url]、[アーカイブ]）です。

FAQにお答えしましょう。1つ目は「実際には流行が大きくなったら人流が減って皆も接触を避けるから、ワクチンの成分だけを機械的に扱うのは反事実ではない。過大評価では？」→誤りです。ご指摘はもっともですが予防接種の「ある」「なし」の差分は予防接種のみを加味して計算すべきものです 続）

西浦氏は投稿で、

「実際には流行が大きくなったら人流が減って皆も接触を避けるから、ワクチンの成分だけを機械的に扱うのは反事実ではない。過大評価では？」→誤りです。ご指摘はもっともですが予防接種の「ある」「なし」の差分は予防接種のみを加味して計算すべきものです

などと述べています。

この投稿は、「誤りです」「ご指摘はもっとも」「と計算すべきもの」と述べていて、論旨を把握しにくいところがあります。

西浦氏の投稿に（ ）で私の補足を追加し、論旨を把握しやすくしたものが以下です。

「実際には流行が大きくなったら人流が減って皆も接触を避けるから、ワクチンの成分だけを機械的に扱うのは（論文が計算するべき）反事実ではない。（論文の計算は）過大評価では？」→（計算したシナリオが論文が計算するべき反事実ではないとの指摘は）誤りです。（実際には流行が大きくなったら人流が減って皆も接触を避けるとの）ご指摘はもっともですが（論文が計算する）予防接種の「ある」「なし」の差分は（（４）節 の説明のようにシナリオ作成に関する制約があるので）予防接種のみを加味して計算すべきものです

これなら西浦氏の投稿は（ある程度まで）論旨を把握できます。もう少し説明します。

投稿はまず、「ワクチンの成分だけを機械的に扱うのは反事実ではない」としています。反事実ならばどのようなシナリオを作っても構わないはずと考えると、直後に西浦氏が「誤りです」と否定しているのは腑に落ちません。しかし、（４）節 に述べたように論文が作成できるシナリオに制約があることを考慮するとともに、「ワクチンの成分だけを機械的に扱うのは（論文が計算するべき）反事実ではない。」と補足すると、論旨を把握できるようになります。

補足したその部分は、（２）節 で説明した意味において、「（論文が計算しているシナリオは不自然なので、）それは計算対象とすべき反事実シナリオではない」という質問者の主張を示しています。この主張に対して西浦氏は、（４）節 の意味で「（シナリオは不自然かも知れないが、実質的に不自然なシナリオしか作成できないのだから、計算対象とすべきシナリオではないとの主張は）誤り」と述べています。西浦氏が「実際には流行が大きくなったら人流が減って皆も接触を避ける」に「ご指摘はもっともですが」と答えているのは、（２）節 で説明した通り、それが本来の人々の自然な行動だからです。その後の「予防接種の「ある」「なし」の差分は予防接種のみを加味して計算すべきものです」は、（４）節 で説明した「シナリオの制約があるために、（ワクチンなしシナリオは）予防接種のみを加味して計算するしかない」との事情を述べています。

これで西浦氏の投稿の意味が分かるようになってきました。

ただし、このように多くを補足しなければ論旨を把握しにくい西浦氏の投稿は適切とは言えません。特に、「誤りです」と「もっとも」が何を指しているのか曖昧なので論旨を把握しにくくなっています。

本節で行った補足は私の考えです。投稿を、より一貫して把握できるものがあるならば、伺いたいと思います。よろしくお願いします。

(7-2) 二つ目の投稿

二つ目の投稿はこちら（[url]、[アーカイブ]）です。

「6千万人くらい人口の約半分が感染した場合は重症患者が収容しきれない。入院できないと患者を助けられなくなって致死率が高くなる。過小評価では？」→　誤りです。現実的に致死率が高くなる影響は医療提供体制の限界によって起こるもので、予防接種の「ある」「なし」の因果推論とは無関係　了）

「6千万人くらい人口の約半分が感染した場合は重症患者が収容しきれない。入院できないと患者を助けられなくなって致死率が高くなる。過小評価では？」→　誤りです。現実的に致死率が高くなる影響は医療提供体制の限界によって起こるもので、予防接種の「ある」「なし」の因果推論とは無関係

との投稿を検討すると、西浦氏がこの論文の計算値を「現実的」なものだと考えていないことが分かります。

西浦氏は「人口の約半分が感染した場合は重症患者が収容しきれない。入院できないと患者を助けられなくなって致死率が高くなる。」との懸念に対し、「現実的に致死率が高くなる」ことを認めています。

西浦氏はこの論文の計算に、「（感染が大幅に拡大した時に）現実的に致死率が高くなる」という効果を算入していません。投稿の西浦氏はこの効果を計算で考慮しなくていいと述べていますし、論文の致死率はシナリオによって変化しないからです [注7-2a]。西浦氏に、この論文で「現実的」な死者数を計算しようという意図はないのです。したがってこの論文の感染者数も現実的な計算値は意図していません。（各年齢層で死者数と感染者数は比例するからです。）

西浦氏は、本稿が指摘する 「論文の感染者数と現実の感染者数を比較する誤り」 を、別の形で確認したことになります。

なお、この論文が現実的な値の死者数や感染者数の計算を意図していないなら、西浦氏はそのことを論文の限界事項（limitations）に書くべきでした。また、医療提供体制の限界を考慮しないなら、西浦氏はこの点も limitations に書くべきでした。これらは x.com にではなく、論文に書くべきことです。


[注7-2a] 論文式(12) や、補足情報（41598_2023_44942_MOESM1_ESM.docx）の Supplementary Figure S11 にあるように、感染者死亡率 \lambda_a は、感染者報告率と年齢層 a で変化しますが、シナリオでは変化しません。

(7-3) 三つ目の投稿

三つ目の投稿はこちら（[url]、[アーカイブ]）です。

これらは単なる知的体操の問題なんですが、要するに「他の条件が全部一緒だとして、予防接種だけなかった場合に」というのを非現実的だとしても仮想的に作っているということですよね。そのような仮想に加えて、現実にあわせた仮想も政策判断では重要になりそうですが。

これらは単なる知的体操の問題なんですが、要するに「他の条件が全部一緒だとして、予防接種だけなかった場合に」というのを非現実的だとしても仮想的に作っているということですよね。そのような仮想に加えて、現実にあわせた仮想も政策判断では重要になりそうですが。

この投稿は、本稿の論旨と比較的整合性が高いです。

西浦氏の投稿は、まず一つ目の投稿や二つ目の投稿を指して（したがって論文についての疑問を指して）、

これらは単なる知的体操の問題なんですが、

としています。西浦氏は単に「知的体操」と述べていますが、これはより分かりやすく「専門家間における知的体操」と書くべきでした。これは誤解されやすい特殊な論文であり、専門家間でのみ議論されるべきものと言えるからです。この三つ目の投稿は、この点の説明を意図したのかも知れませんが、投稿の表現だとこの意味はほとんど伝わりません。西浦氏は「知的体操」と書いた含意を、より明確にすべきでした。専門家である西浦氏と同様の知的体操を、一般の人が行う必要はないからです。

投稿はその後、論文のシナリオについて以下のように述べています。

要するに「他の条件が全部一緒だとして、予防接種だけなかった場合に」というのを非現実的だとしても仮想的に作っている

西浦氏はここで、論文が仮想的に作ったシナリオが「非現実的だ」と、述べています。これは本稿が（２）節の「雨と傘の例え」 などで説明した内容であり、この論文の最も重要な性質を示しています。西浦氏はこの点を論文でより丁寧に説明すべきでした。

また西浦氏はここで、論文のシナリオを「他の条件が全部一緒だとして、予防接種だけなかった場合に」と表現しています。これは、(5-2)節 に説明した論文式(3) そのものです。当たり前のことですが、西浦氏の投稿は、論文の数式と整合しています。

投稿はその後、

そのような仮想に加えて、現実にあわせた仮想も政策判断では重要になりそうですが。

と述べています。ここでも西浦氏は、論文の仮想シナリオが「現実にあわせた」ものではない（論文の仮想シナリオは非現実的なものだ）と、本稿（２）節 が示した内容を実質的に繰り返しています。ただし西浦氏は、現状の Sci Rep 2023 論文も政策判断で重要であるかのように書いていますが、この論文の計算結果は（専門の学会ですら誤解するほど）極めて誤解されやすいものです。この論文を政策判断に用いるのは、誤解を招かないようにしてからにするべきです。

（８）Sci Rep 2023 論文の意義の再検討

そもそも本稿は、全体として Sci Rep 2023 論文の意義を検討していますが、本節では特に、他であまり検討してこなかった二つの事項について述べます。

(8-1) Sci Rep 2023 論文の計算結果が政策判断の助けになるかは疑問

一般に、ある論文が何らかの値を推定した場合、その値が正確でなくても、政策判断の助けになることはあります。しかし Sci Rep 2023 論文はそうした論文に該当しないと思われます。

この論文の推定値が政策判断の助けになるには、その推定値がどの程度信頼できるのかについての情報が少なくとも必要です。論文は、Figure 1 などで 95% 信頼区間を示しているので、これを示しているようにも見えます。

しかしこの論文のように「全て」がモデルに基づく計算での信頼区間は、そもそも信頼区間計算の妥当性が自明ではなく、不適切な信頼区間を計算することさえ可能です。したがって西浦氏は、信頼区間の正当性を示すためには、信頼区間計算の詳細を開示する必要があります。しかし論文はこれを開示していません。 だから論文に書かれている信頼区間の信頼性は、不明です。

またそもそも、行動変化と実効再生産数との関係が不明であることを示した（４）節 の検討を踏まえると、この論文の感染者数の推定値がどの程度過大なのかは、論文著者にも不明です。どの程度過大なのか不明な推定値についての信頼区間は、仮に計算されたとしても信頼できる数値にはなりません。またどの程度過大なのかが不明な推定値が政策判断の助けになるかが疑問であることは、ご説明するまでもありません。

さらに (4-1)節 で検討したように、Sci Rep 2023 論文には現実社会をモデル化しようとの意図が最初からなかったと考えられますし、(7-2)節 で検討したように、西浦氏は投稿でも現実的な計算の意図を実質的に否定しています。

このような論文の推定値を政策判断に使うことは、妥当ではありません。

(8-2) 一般の人にとって Sci Rep 2023 論文とは

Sci Rep 2023 論文のような計算を専門家が行い、それを論文として報告することは、仮に論文の内容に問題があったとしても一定の意味があるのかも知れません。

しかしこの論文は、想定が不自然で非現実的な論文・計算であり、過大な感染者数を計算している上にそれが明示されていません。これは一般の人が内容を見聞して理解することが要請されたり、奨励されたりするような論文ではありません。論文が推定値の過大さを明示していないので、一般の人はその結果を現実の感染者数と比較してしまう恐れがあります。

およそ論文というのは専門的なのですが、この論文はとりわけ特殊で専門性の高い論文です。したがって一般の人がこの論文に注目する必要はなく、この論文は「専門家間の知的体操」だと考えるのが適切です。

（９）論文への誤解の原因と西浦氏の責任

(9-1) Sci Rep 2023 論文の説明不足と、それによる誤解の拡散

Sci Rep 2023 論文についての誤り（「論文の感染者数と現実の感染者数を比較する誤り」）が広がった背景には、主に四つの要因があります。

一つ目は、論文が採用している論理が誤解されやすいことです。専門家がその専門分野における被害想定を計算する際、（実現しないことがはっきりと分かっている）非現実的な想定で計算することはほとんどありません。（論文がこのような特殊な計算をした理由が理論的な限界のためであることは、（４）節 で説明しました。）

二つ目は、論文が誤解されやすいポイントを分かりやすく説明していないことです。西浦氏にとって、この論文が誤解されやすいことは、意外ではないはずです。本稿が指摘しているこの論文についての誤り（「論文の感染者数と現実の感染者数を比較する誤り」）は、このような論理構成の論文では予想される誤りです。したがって西浦氏は、この論文が誤解されないよう、充分に注意を払うべきでした。論文がこの点を明確にしていれば、誤解を防ぐ余地はあったはずです。

三つ目は、論文自体ではなく西浦氏による x.com への投稿の問題です。西浦氏の投稿は、本節の一つ目、二つ目の問題による論文の誤解を正すのではなく、むしろ誤解を招いています。論文の誤解されやすさを最もよく知る西浦氏による不適切な投稿ですから、その責任は大きいです。

四つ目は、論文に関して述べられるその他の言説です。産経記事が誤り、約一年後には専門家の集団である三学会も誤りを含む見解を出しています。

このように拡散された誤解は、ワクチンへの「優良誤認」を引き起こし、ワクチンへの過剰な期待や誤った判断に基づくワクチン接種を招く可能性があります。また、専門家や専門家集団の説明責任が果たされていないことは、政策決定者や一般市民に不信感を与える可能性があります。

(9-2) 西浦氏が説明すべきこと

論文の著者である西浦氏は、Sci Rep 2023 論文の非現実的な想定やその計算結果の考え方について、明確で丁寧な説明を行い、日本社会に広がっている誤解を解消する責任があるのではないでしょうか。

具体的には、

  • ワクチンなしシナリオが不自然で非現実的な想定のシナリオであること。（２）節。
  • 論文が計算する感染者数や死者数が、現実的な値を意図したものではないこと。(4-1)節、(7-2)節。
  • 論文が計算する感染者数や死者数が、過大な値だと分かっていること。(2-2)節。
  • 論文が計算する感染者数と現実の感染者数を比較してワクチンの効果だと述べてはいけないこと。(3-5)節。
  • 論文を根拠とした不適切な記述のある産経記事は修正すべきであること。(6-3)節。
  • 論文を根拠とした不適切な記述のある三学会の見解は修正すべきであること。(6-5)節。
  • 論文が政策判断の助けになるかは疑問であること。(8-1)節。

を改めて説明すべきです。

（１０） 政府や企業の対策に関するシナリオの問題点

ここで述べるのは、「雨と傘の例え」では煩雑になるので省略した事項です。

Sci Rep 2023 論文の考え方では、ワクチンなしシナリオでの政府や企業などの対策は、現実と同じ時に同じ対策を実施すると考えます。例えばワクチンなしシナリオで緊急事態宣言を開始した日、終了した日は、現実で宣言を開始した日、終了した日と同じです。ワクチンなしシナリオでどんなに感染が拡大しても、現実と同じ日より早く宣言を開始することはありません。また感染の拡大状況に関わらず、現実と同じ日には宣言を終了します。この点を「雨と傘の例え」では省略しましたが、これを含めて検討してもますますワクチンなしシナリオが不自然になるだけなので、省略したことによる本稿の論旨への影響はありません。

（１１） [Kayano 2023b] における、Sci Rep 2023 論文と同じ構造の問題

西浦氏は、2023-10 に複数の論文を発表しました。本稿で検討してきた、全国での感染者数などを論じた Sci Rep 2023 論文 [Kayano 2023a] と、東京での感染者数などを論じた別の論文 [Kayano 2023b] です [注6-5b]。 [Kayano 2023b] も仮想シナリオを構築し、そこにおけるワクチン接種率を仮想的に変更してワクチンなしシナリオを作成し、そこでの感染者数を推定しています。

[Kayano 2023b] のシナリオには、Sci Rep 2023 論文のシナリオと同じ問題があります。「ワクチンなしになったことで感染者数が増大しているのに、人々の行動などが変化しない」との不自然で非現実的なシナリオだという問題です。 したがって [Kayano 2023b] の推定値を、現実の感染者数と比較することも不適切です。ところが (6-5)節 で述べた三学会の見解は、この論文にも言及していて、関係する部分は

また、オミクロン株流行期の2022年1月から5月の東京都でも、直接的・間接的に感染者数を65%減少させたと報告されています { }^{3)}。

となっています。"3)" が [Kayano 2023b] を参照しています。この引用部は、この論文の推定感染者数を現実の感染者数と比較しているので、(3-5)節 に示した「論文の感染者数と現実の感染者数を比較する誤り」 に陥っています。

したがって三学会の見解のこの部分も不適切です。

（１２） 結論

本稿は、Sci Rep 2023 論文が想定する『ワクチンなしシナリオ』が不自然で非現実的であることを指摘し、その計算結果が現実の感染者数や死者数と比較されることの問題点を明確にしました。

論文のワクチンなしシナリオがどれほど現実的でないかを、「雨と傘の例え」で説明しました。小雨で傘を差していた人が、大雨で傘がなくても同じ行動をするなどのシナリオは、感染拡大に伴う行動の変化を無視しています。これは不自然であり非現実的です。

その結果この論文が計算する感染者数は過大になっています。論文の計算結果を現実的なものとして扱うべきではなく、論文の計算結果に言及する場合には、この想定の特殊性を踏まえる必要があります。

Sci Rep 2023 論文の計算結果を扱う場合によくみられる誤解として、「論文の感染者数と現実の感染者数を比較する誤り」を示しました。論文の「ワクチンなし」の推計感染者数を現実の推計感染者数と比較し、それをワクチンの効果とするのは不適切です。

産経記事や三学会（日本感染症学会、日本呼吸器学会、日本ワクチン学会）の見解は、この論文の特殊な想定を説明せずにその計算結果を現実の感染者数と比較し、ワクチンの効果としています。したがって「論文の感染者数と現実の感染者数を比較する誤り」に陥っています。これにより、読者や政策決定者がワクチンの効果を過大評価する可能性があります。

この論文は、「ぜひ多くの方に読んでいただきたいニュースです」などと一般読者に向けて推奨されるような論文ではありません。この論文が扱うシナリオは不自然で非現実的な想定に基づいているからです。計算結果を紹介する際には、その特殊性を充分に説明し、誤解を避ける責任があります。

Sci Rep 2023 論文の誤解がこれ以上拡散することを防ぐには、論文著者である西浦氏や学会が、論文の想定や計算の結果の限界について積極的に説明する必要があります。そして、政策決定者や社会に誤った印象を与えないよう努めるべきです。

（参考文献）

[Kakeya 2024] H. Kakeya, M. Itoh, Y. Kamijima, T. Nitta, and Y. Umeno, "Unreliability in Simulations of COVID-19 Cases and Deaths Based on Transmission Models," medRxiv, preprint, Feb. 2024. [Online]. Available: https://doi.org/10.1101/2024.02.02.24302123.

[Kayano 2023a] N. Kayano and H. Nishiura, "Evaluating the COVID-19 vaccination program in Japan, 2021 using the counterfactual reproduction number," Scientific Reports, vol. 13, no. 1, article 17265, 2023. [Online]. Available: https://doi.org/10.1038/s41598-023-44942-6.

[Kayano 2023b] T. Kayano and H. Nishiura, "Assessing the COVID-19 vaccination program during the Omicron variant (B.1.1.529) epidemic in early 2022, Tokyo," BMC Infectious Diseases, vol. 23, no. 1, p. 746, 2023. [Online]. Available: https://doi.org/10.1186/s12879-023-08748-1.

[Nakamura 2024a] T. Nakamura, "Transmission model and arithmetic of dynamical systems," ResearchGate, [Online]. Available: http://dx.doi.org/10.13140/RG.2.2.12968.99840/1. [Accessed: Dec. 21, 2024].

[Nakamura 2024b] T. Nakamura, "Remarkable data in Kayano T, Ko Y, Otani K, et al.," ResearchGate, [Online]. Available: http://dx.doi.org/10.13140/RG.2.2.22188.68489. [Accessed: Dec. 21, 2024].

（付録）

(付録Ａ) 本稿に関係のある url など

  • 本稿に言及している x.com のスレッド [url]（まだ書いてません。）

(付録Ｂ) 本稿に出てくる url とアーカイブ

参考文献以外の url とアーカイブのリスト。本文中に示したものもあります。

  • 2023-10-18 西浦氏の x.com への投稿。Sci Rep 2023 論文を紹介したもの。[url] [アーカイブ]
  • 2023-11-01 西浦氏の x.com への投稿。「FAQにお答えしましょう」「非現実的」「知的体操」を含む3つの投稿によるスレッド。[url] [アーカイブ]、[url] [アーカイブ]、[url] [アーカイブ]
  • 2023-11-16 産経記事「新型コロナワクチンで死者９割以上減　京都大推計」 [url] [アーカイブ]
  • 2023-11-16 共同記事「コロナワクチンで死者9割以上減　京都大チームが推計」 [url] [アーカイブ]
  • 2023-11-16 西浦氏の x.com への投稿。「ぜひ多くの方に読んでいただきたい」など [url] [アーカイブ]
  • 2024-10-17 日本感染症学会、日本呼吸器学会、日本ワクチン学会「2024年度の新型コロナワクチン定期接種に関する見解」 [url] [アーカイブ]
  • 2024-10-17 日本感染症学会、日本呼吸器学会、日本ワクチン学会「2024年度の新型コロナワクチン定期接種に関する見解（概要版）」 [url] [アーカイブ]
  • 2024-10-21 上2件へのリンクがある日本感染症学会のお知らせ [url] [アーカイブ]
  • 幾つかの図版は [url] 以下を参照しています。

    （更新履歴）

  • 2024-12-17
    公開。
  • 2024-12-20
    (6-5)節 に、「西浦氏の別の論文 [注6-5b]」と書いていましたが、「西浦氏の別の論文 [Kayano 2023b]」が正しい表現だったので修正しました。
  • 2024-12-21
    以下の修正を行いました。これらによる論旨の変更はありません。
    • (2-1)節 の「反事実シナリオ」との表記を「反事実仮想シナリオ」に修正しました。
    • (2-1)節 の末尾に、「またこの例えは、」から「済んでいます」までを追記しました。
    • (2-4)節 を追加しました。
  • 2024-12-22
    [Nakamura 2024a]、[Nakamura 2024b] を参考文献に加え、これらの紹介を（１）節 に加えました。
  • 2024-12-25
    以下の修正を行いました。これらによる論旨の変更はありません。
    • (2-5)節 を追加しました。
    • (2-4)節 の見出しを、(2-5)節との対比を考慮して変更しました。